Bob Kåres homepage

Best viewed with any browser

Algorithm for icon placement on polygons

This algorithm finds a point for placement of an icon (or a label) which is guaranteed to be inside of a polygon and somewhere towards the center of the figure.

As input the algorithm only requires the vertices as an ordered list.

Step 1: Find points halfway inside the polygon

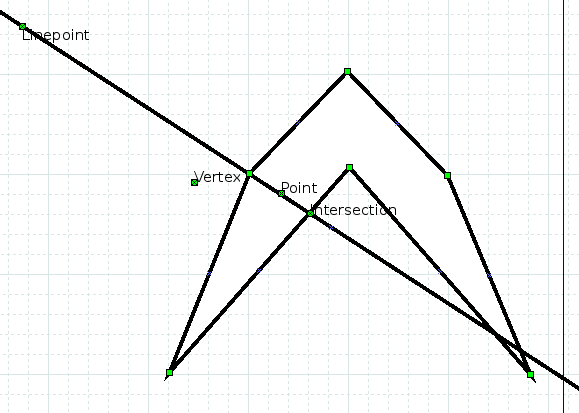
Explanatory figure for step 1

Figure 1: Explanatory figure for step 1

For every vertex we find a point halfway inside the polygon.

Step 1.1: Find angle

First we find a angle between vertex-1 and vertex+1 through vertex. We then imagine a line through vertex along the half-point of this angle. Implemented using atan2 this is done as follows: 

from = vertex-1
through = vertex
to = vertex+1

from_x = from_x - through_x
from_y = from_y - through_y

to_x = to_x - through_x
to_y = to_y - through_y

from_angle = atan2(from_y, from_x)+pi
to_angle = atan2(to_y, to_x)+pi

angle = min(from_angle, to_angle) + ( max(from_angle, to_angle) - min(from_angle, to_angle) )/2

Step 1.2: Linepoint

We then create an imaginary point "linepoint" along this line, so that we have two coordinate pairs to work with when finding intersections. This can be done with x = x + cos(angle), y = y + sin(angle). 

a = 180 - vertex_x
b = a * tan(angle)

linepoint_x = vertex_x + a
linepoint_y = vertex_y + b

Step 1.3: Find intersections with edges

The next step is then to find all intersections between the line vertex-linepoint and the edges of the polygon. We need to have a total count of intersections in at least one direction from vertex to determine which way points towards the inside of the polygon (ray-casting point in polygon algorithm). We also need the closest edge in that direction.

To handle polygons with holes we just include the hole-polygons in the list of edges we check against.

In psuedocode: 

foreach E in edges and hole_polygon_edges
  skip if E_from == vertex or E_to == vertex

  skip unless intersection = find_intersection(vertex-linepoint, E_from-E_to)

  skip unless point_on_segment(intersection, E_from-E_to)

  distance = distance(vertex, intersection)

  if point_on_segment(intersection, vertex-linepoint)
    intersectioncount++
    if distance < nearestOn_distance
      nearestOn = intersection
  else
    if distance < nearestOff_distance
      nearestOff = intersection

Step 1.4: Find point

Now we can finally calculate the point by taking the nearest intersection point in the right direction (looking at intersectioncount to find out which direction) and getting the point halfway between vertex and the intersection.

In psuedocode: 

if intersectioncount % 2 == 0
  point = nearestOff
else
  point = nearestOn

point_x = vertex_x + (point_x - vertex_x)/2
point_y = vertex_y + (point_y - vertex_y)/2

Step 2: Get centerpoint

Now we use the points halfway inside the polygons to find a point to place the icon.

This part of the algorithm could do with some work, I have ideas for several approaches that should be tested on various polygons to find the best one.

Some random ideas: